泰祺教育

平面几何是管综数学中非常重要的内容，是几何的基础和核心，主要考查三角形、四边形、圆、扇形等基本平面图形的角度、长度和面积。接下来，给大家具体展示一下近五年平面几何的考试题型以及考点分布。

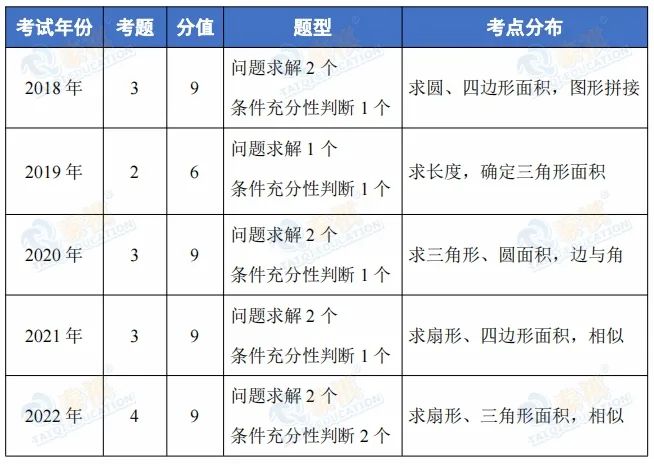
从上图我们可以总结得出：平面几何每年一般会考2~3题，并且求图形的面积是必考考点。因此掌握好基本平面图形的面积求法就显得尤为重要，所以本篇文章先带大家梳理一下平面几何之三角形面积的破解方法。

我们先来看一下在求三角形面积时会涉及到的数学公式：

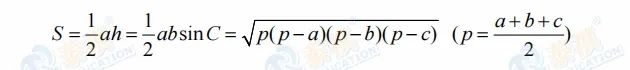
以上是求三角形面积的三个基础公式，但是在考试中我们会发现平面几何的难点主要在于图形的变换，所以除了要掌握基本的公式外，还要懂得如何快速破题。接下来要给大家介绍关于破解三角形面积的“四大金刚”。

等积模型

（1）等底、等高的两个三角形面积相等.

（2）两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比．

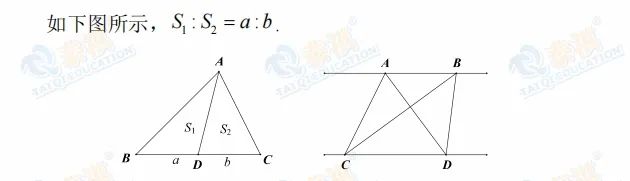
（3）夹在一组平行线之间的两个三角形，若底相等，则面积相等．

共角模型（鸟头定理）

（1）共角模型：

两个三角形中有一个角相等或互补，这两个三角形叫作共角三角形，共角三角形的面积比等于对应角（相等角或互补角）两夹边的乘积之比．

（2）常见类型：

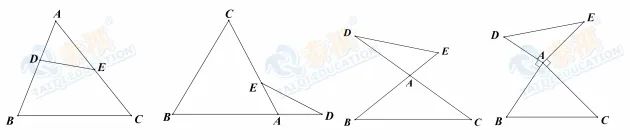
（3）在以上四个图形中

相似模型

共边模型（燕尾定理）

通过以上几道例题，我们可以发现三角形面积的求解方法还是比较多的，同时要求我们学会根据不同图形灵活选择合适的计算公式或者模型。所以在平面几何的学习中，我们首先要掌握基本的求解公式，并且还要多归纳多总结几何模型，寻找做题的突破口。

今天梳理的四大模型，同学们都学会了吗？希望大家能学以致用，灵活解决三角形面积的求解问题，在联考数学中取得好成绩！